今回の記事は当直中の暇つぶしに行った実験についてです。
一般撮影において管電圧やmAs値はもちろん、撮影距離やX線中心も画像に大きな影響を与えます。距離は拡大率やX線量に、X線中心は投影像の流れに影響を与えます。
不適切な手技により撮像されたX線画像では誤った診断をしてしまう可能性があります。
しかしながら撮影距離やX線中心の情報は画像(DICOMタグ)には残りません。
※撮影距離はプロトコルの初期設定の固定値が記録されているかもしれません。
画像の中に照射野の4辺が映っていれば、X線中心を特定することもできますが、
いつもそのような注意を払うのは面倒です。
そこで今回はX線中心を推定する仕組みを考えていきます。
(撮影距離はまた今度)
色々な方法があると思いますが、今回は2つの鉛玉がずれて投影されることを利用します。ずれた方向からX線中心を推定していきます。
鉛玉を2つ受像面から離して配置します。鉛玉に向けて垂直入射した場合は完全に重なり、少しでも斜めに入射した場合は2つに分かれて投影されます。
受像面から遠い方の鉛玉は、近い方の鉛玉よりも遠くに投影され、2つの鉛玉を結ぶ直線上にX線中心があるということになります。
(理想条件ではね)
この仕組みを2か所で行えば2つの直線の交点からX線中心を推定できるのでは?という試みです。
では実際にやってみます
下の写真に示すように17×17インチの受像面に25か所、シールを貼りました。
ですが、管球が端まで動かなかったので左側の4列(16か所)をX線中心として使います。
鉛玉2つを受像面から垂直にズレがないよう配置しようと思ったのですが、これが非常に難しい。
試行錯誤した結果、最終的には院内にあるテープに張り付けることにします。距離は2cm離しておきました。こんなに離さなくてもいいかも。
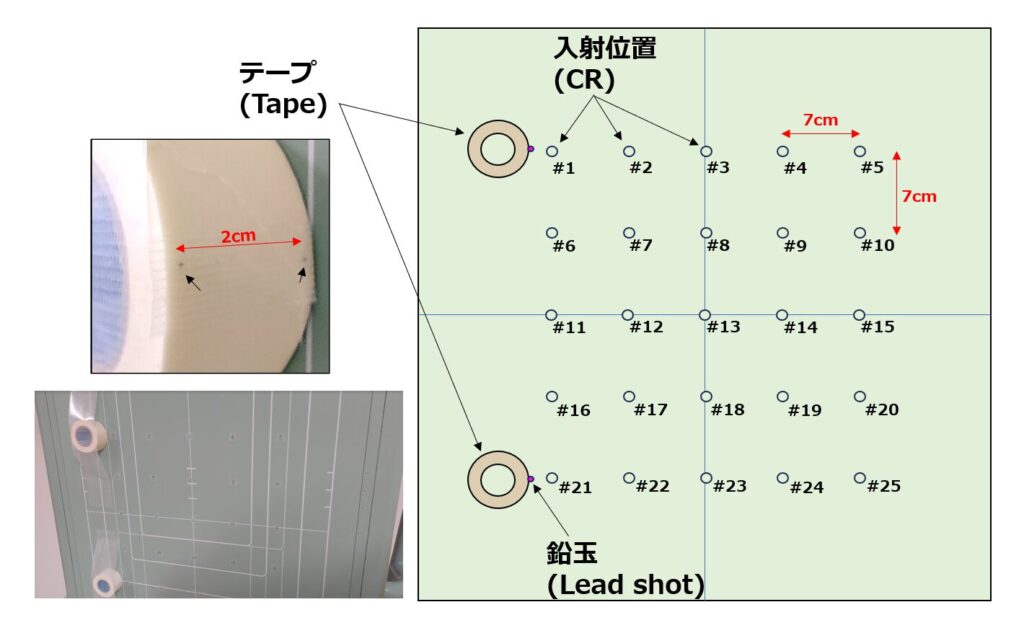
照射野が開かなかったので今回は距離を200cmとしました。撮影距離が近い方が鉛玉がずれて投影されるはずなので200cmで可能であれば100cmでも可能だと思います。
撮影条件は50kV, 10mAsとしました。
ではX線中心を#1にして撮影します
得られた画像です。それぞれ上のテープ、下のテープの部分を拡大したものを画像の左に表示しています。
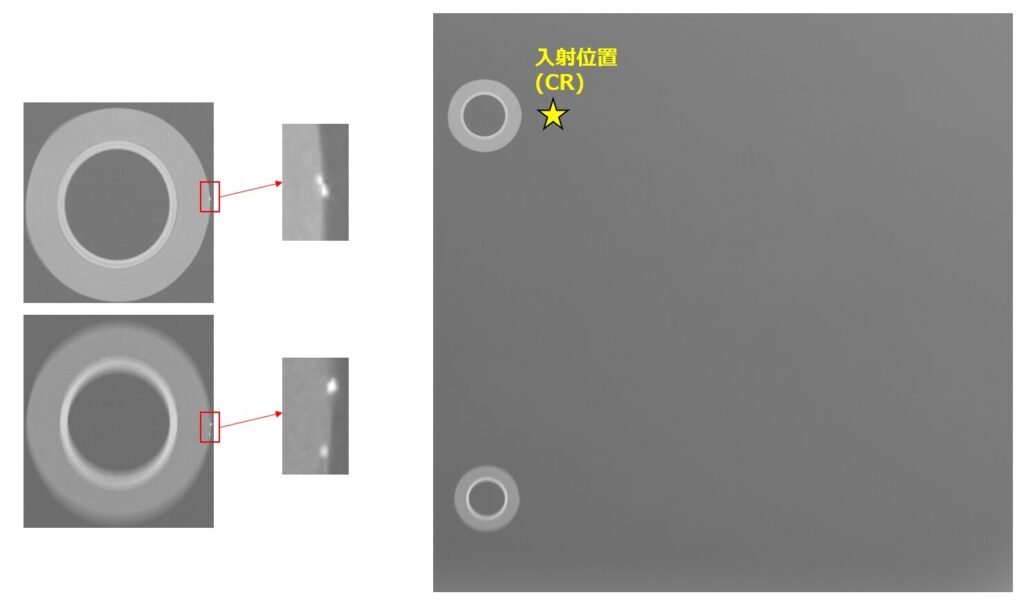
X線中心を#1とした場合、上のテープに貼った鉛玉のずれは最も小さくなるはずですが、少しズレているようですね。X線中心は鉛玉と、ほぼ同じ高さなのに上下にズレがあるということは鉛玉の配置がいまいちだったことが分かります。(そしてこれが推定位置の精度にめっちゃ影響します)
下のテープに貼った鉛玉は予想通り上下にずれて投影されています。
まぁやり直している時間はないのでこのまま進めます。
では、ズレた鉛玉を結ぶように線を引いてみましょう。
本当はプログラムを書いて自動的に鉛玉2点を通る直線を引くべきなのでしょうが、プログラムを書いてる時間もないのでそのまま手動でやります。

本来のX線中心との誤差は6.3cmでした。
では続けて#2から#24まで撮影、X線中心を推定していきます。結果は以下のようになりました。座標は画像の左上を原点としています。

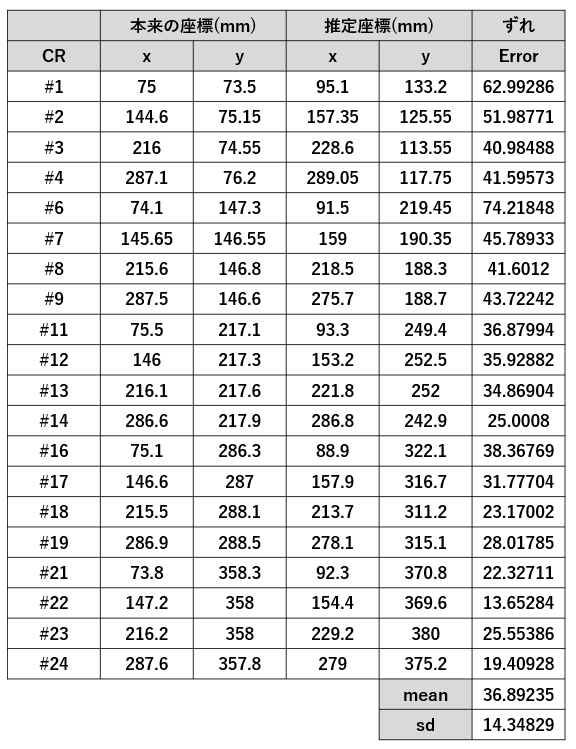
推定した座標はほぼ全て、本来の位置よりも下側になりました。これは上のテープに張り付けた鉛玉の上下のズレが原因です。
やっぱり最初に試し撮りして位置を修正するべきだった・・・
誤差としては36.9±14.3mmって感じでした。
まあ4cm程度のずれで推定できれば満足ですが、鉛玉の配置をしっかりしておけばもっと精度は出ていたでしょうね。
今回はテープにしましたがマーカーに貼ったりすれば実用性があるかもしれません。そもそも装置の内部にこういう機構があれば自動的にX線中心を推定してくれると思うのですが。
撮影距離に関しては、X線中心が推定できたあとに鉛玉の距離から推定できると思います。機会があれば今度やってみようと思います。
ちょうど当直も終わりに近づいてきたので、終わりにしたいと思います。
ご覧いただき、ありがとうございました。
追記
結局、画像を整えたり清書したほうがいいと思ったので当直中にアップはできませんでした。
追記2
鉛玉がズレて配置されていたことで推定精度が悪くなってしまいましたが、既知の測定データがあれば補正可能だと思い、追加の検証を行いました。
こういう補正はX線検査装置のいたるところで使われてますよね。キャリブレーションっていうやつでしょうか。
#1・#4・#21・#24のデータを使って補正しました。
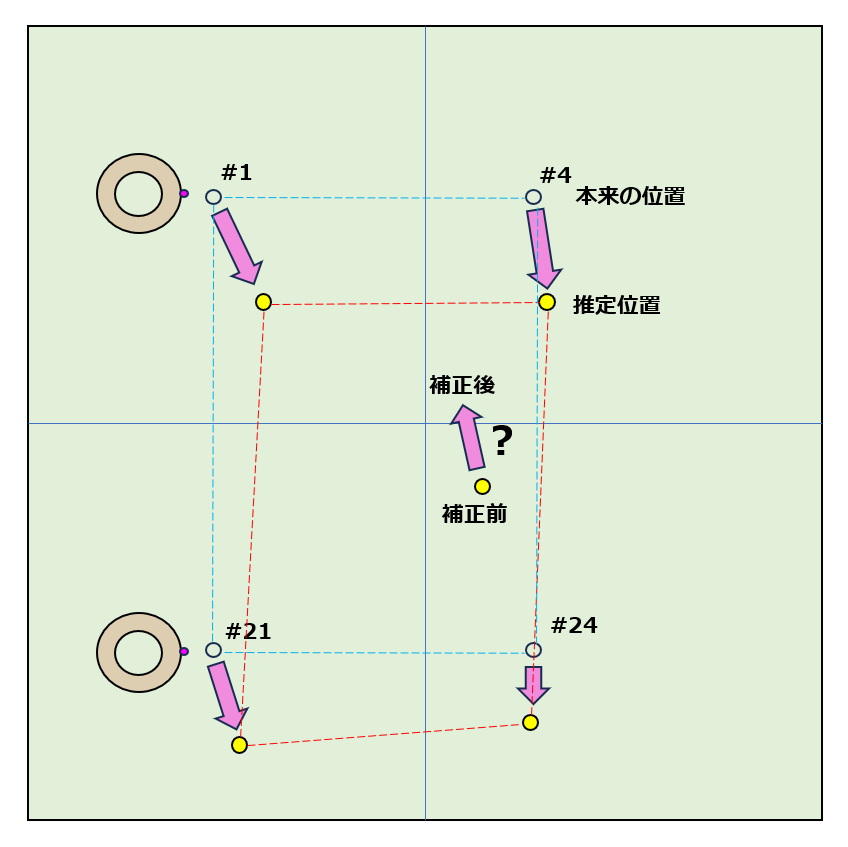
このような補正には双線形補間を使います。
以下はpythonでの実装です。
from scipy.optimize import minimize
# 入力座標と出力座標の定義
xa, ya = 75, 73.5 #1 True
output_xa, output_ya = 95.1, 133.2 #1 Estimated
xb, yb = 287.1, 76.2 #4 True
output_xb, output_yb = 289.05, 117.75 #4 Estimated
xc, yc = 73.8, 358.3 #21 True
output_xc, output_yc = 92.3, 370.8 #21 Estimated
xd, yd = 287.6, 357.8 #24 True
output_xd, output_yd = 279, 375.2 #24 Estimated
# 補正前
target_x, target_y = 213.7, 311.2 #18 Estimated
# 双線形補間関数
def bilinear_interpolation(z):
zx, zy = z
# 正規化
norm_zx = (zx - xa) / (xb - xa)
norm_zy = (zy - ya) / (yc - ya)
# X方向の補間
R1x = output_xa + (output_xb - output_xa) * norm_zx
R2x = output_xc + (output_xd - output_xc) * norm_zx
# Y方向の補間でXの出力
Zx = R1x + (R2x - R1x) * norm_zy
# Y方向の補間
R1y = output_ya + (output_yb - output_ya) * norm_zx
R2y = output_yc + (output_yd - output_yc) * norm_zx
# Y方向の補間でYの出力
Zy = R1y + (R2y - R1y) * norm_zy
return Zx, Zy
# 目的関数:実際の出力と推定出力との差の二乗和
def objective_function(z):
Zx, Zy = bilinear_interpolation(z)
return (Zx - target_x) ** 2 + (Zy - target_y) ** 2
# 初期推定値(大まかな中心点)
initial_guess = [(xa + xb + xc + xd) / 4, (ya + yb + yc + yd) / 4]
# 最適化の実行
result = minimize(objective_function, initial_guess)
print(result.x)これを使って#7, #8, #12, #13, #17, #18を補正してみました。結果を下の表にまとめました。
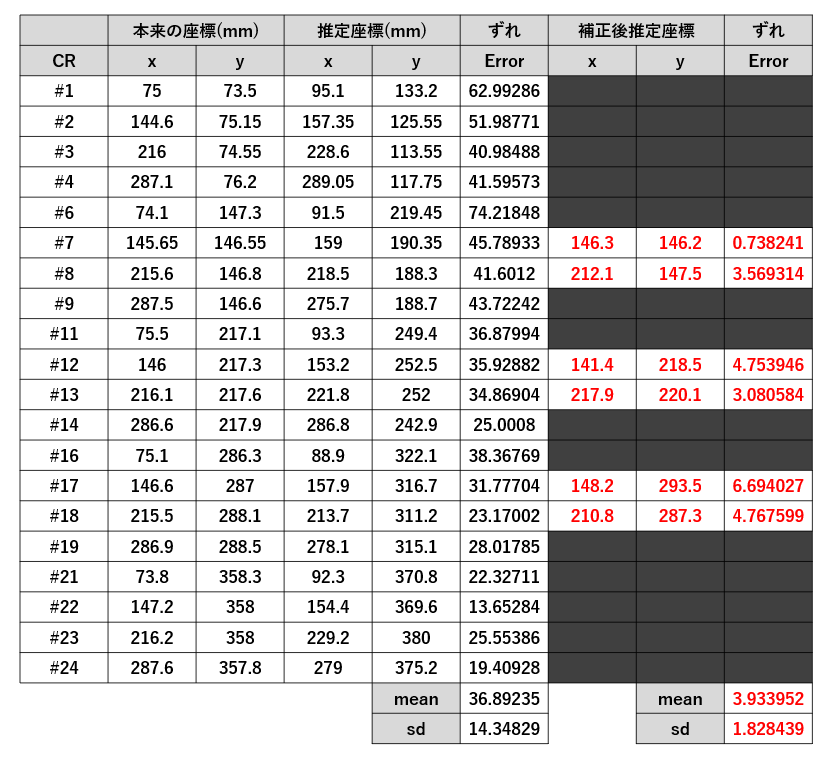
誤差は4mm程度となり、大幅に精度が向上しました。
追記3
もっと良い方法がありましたので、追加の検証を行いました。
処理の流れとしては
①2つの鉛玉を受像面に垂直に離して配置するのではなく、FPDの受像表面に1つだけ貼る。上下の2か所で同様。
②上下それぞれの鉛玉を中心にX線を入射して2枚の画像を取得し、鉛玉の部分を抜き出して1枚にまとめる。(基準画像)
③任意の場所をX線中心にして撮影する。
④上記②と③で得られた画像を重ねて、ズレた鉛玉を結ぶ直線を2本描き、交点を求める。
という感じです。FPDの受像表面から検出部までには数cmの距離があることを利用しています。
以下の写真は実際に受像面に貼った様子です。見なくてもわかるって?

以下は②で得られた基準画像です。

鉛玉が映っているところを拡大するとこんな感じです。
鉛玉を動かさずにそのままX線中心を任意の場所に変えて撮影します。X線中心にも目印として鉛玉を貼っています。
得られた画像と基準画像を加算したのが下の画像です。
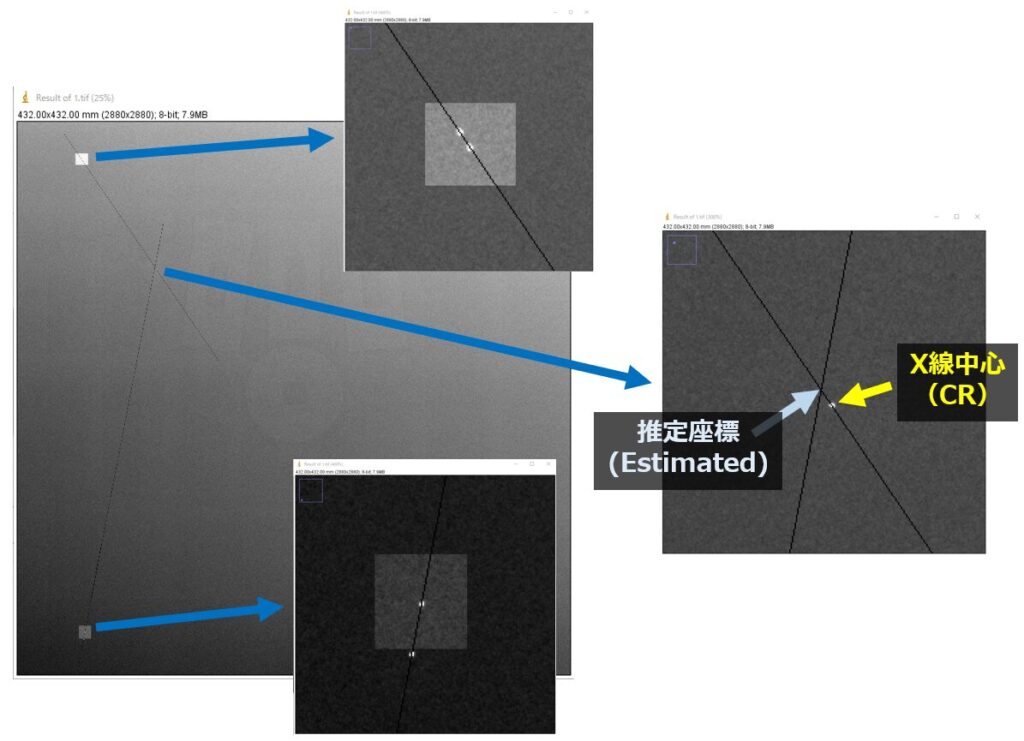
色の変わっている四角の中心(鉛玉の影)がもともとの位置で、もう一つの鉛の影はX線が斜めに入射することで中心からズレて投影されています。
得られた画像からX線中心を推定してみると、正解の座標に近いのが分かります。
その他、9か所で入射点を変えて撮影し、X線中心を推定しました。

誤差は3.86±2.55mmという結果でした。
この方法は簡単に使えるため実用的だと思います。